2*Pi ist rausdividiert, also das Makro berechnet Cos(2*pi*x) für x aus dem Intervall -.5 bis .5. (Bin immer froh, wenn keine Pis in der Struktur rumturnen, und der Wrap ist einfacher).
Ein Trick bei dem hier ist das Ausnutzen einer Symmetrie, das Umklappen an den Peaks (der Betrag macht das oben, hab ewig dran gesessen, das Compare&Routing rauszubekommen). Theoretisch kann man damit schon mit 5 Monomen eine Genauigkeit von <1E-8 erreichen, allerdings müsste man dann alle Parameter gesondert, also nicht über QuickConst (die nach 4 Stellen voll ist), reingeben. So wie ich das mal geprüft hab, sind aber alle 6 im Reaktor angezeigten Nachkomma-Stellen bei dieser Implementierung genau.
Mit noch 3 zusätzlichen Additionen + 3 Multiplikationen (also Order 8 statt 5) kann man rein rechnerisch 1E-15 als Fehler unterschreiten (müsste aber jeden Parameter superexplizit eingeben).
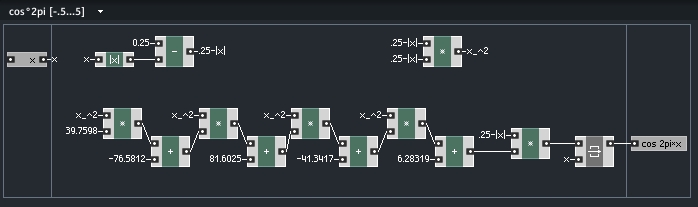
Cosinus (x*2*pi) von -.5 bis +.5
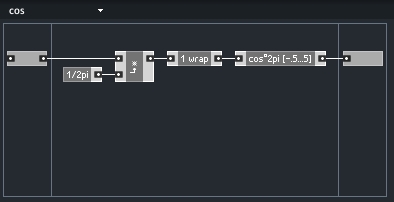
Cosinus (mit Wrapping und normaler Werteeingabe zwischen -pi und +pi):
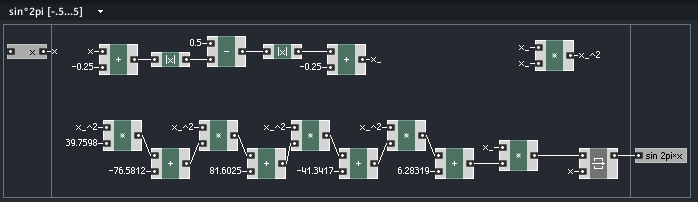
Sinus (x*2*pi) von -.5 bis +.5:
---
Um an die Polynome zu kommen, hab ich länger gebraucht, bis ich auf dieses Script gestoßen bin:
http://metamerist.com/cheby/example38.htm